Cuentan que estando el famoso sabio postrado en el lecho, recibió la visita de A. Moshkovski que para procurarle alguna distracción le propuso el siguiente problema:
Tomemos un reloj que tenga la manecillas a las 12. Cambiando la función de las manecillas, es decir, que el minutero avanzara a la velocidad del horario y viceversa, a las 12 no se
notaría, porque ambas estarían juntas. Pero a otras horas, por ejemplo a la seis, nos resultaría un absurdo, porque el minutero no puede hallarse en la 6 cuando el horario haya recorrido exactamente seis horas. Entonces se puede proponer:
¿Cuándo y cada cuánto tiempo ocupan las manecillas de un reloj normal una posición que al cambiar la función de las manecillas nos den posiciones similares a las normales?
Como no podía falta la anécdota, dicen que Einstein contestó a su interlocutor; “Sí, este problema es muy apropiado para un hombre obligado por su enfermedad a permanecer postrado en su lecho, porque es interesante y no demadiso fácil. Pero me temo que mi distracción me durará poco, porque he dado ya con la forma de resolverlo”.
E incorporándose en el hecho, en pocos trazos dibujo un esquema que reflejaba las condiciones del problema. ¿Cómo se resuelve?
En todo problema relacionado con las manecillas del reloj hay que tener en cuenta las velocidades relativas de éstas. Ambas están en la relación 5/60, o lo que es lo mismo, 1/12. Dividiendo la esfera en 60 divisiones, llamemos x al número de divisiones recorridas por el horario y asimismo, y a las recorridas por el minutero. Advirtamos que siendo nuestros relojes regidos por el sistema sexagesimal, el minutero recorre y divisiones en y minutos, o sea en y/60 horas.
El minutero habrá pasado la cifra 12 hace y/60 horas, en tanto que el horario habrá recorrido x/5 horas, luego: y/5 = x/60
Igualdad que debe ser equivalente a un número entero. Planteando el siguiente sistema de ecuaciones:
y/5 - x/60 = a
RELOJES
Los relojes y su utilidad para la medición del tiempo son motivo de una gran variedad de problemas y acertijos, se clasifican en:
I) Atraso y adelanto
II) Agujas y ángulos
I. ATRASO Y ADELANTO
Situaciones en las cuales, como consecuencia de un mal funcionamiento del reloj, este sufre adelantos y atrasos respecto a la hora que indica un reloj de funcionamiento normal.

¯ Si está atrasado:
Hora Real = Hora Marcada + Atraso
¯ Si está adelantado:
Hora Real = Hora Marcada - Adelanto
II. AGUJAS Y ÁNGULOS
OBS.: El reloj es circular y a manecillas.
1) 60 div <> 360º
1 div <> 6º
2) Entre 2 marcas horarias
5 x 6 = 30º
3) Relación:
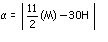
Apliquemos toda este concepto en los problemas de aplicación
DESAFIO Nº1:
Silvia al ver la hora confunde el minutero por el horario y viceversa y dice : “son las 4:42 h”. ¿Qué hora es realmente?
DESAFIO Nº2:
Se tiene 2 relojes, uno se adelanta 3 minutos por hora y el otro se atrasa 2 minutos por hora. Si ambos relojes se les sincronizó el 25 de febrero de un año bisiesto a las 15:00 h. ¿En qué fecha exactamente ambos relojes volverán a marcar la misma hora?
MENSAJE DEL PROFESOR: Si presentas las soluciones de los desafios en una hoja cuadriculada con tu nombre y grado el miercoles a las 8 am obtendras 2 puntos adicionales en el curso
DESAFIO Nº2:
Se tiene 2 relojes, uno se adelanta 3 minutos por hora y el otro se atrasa 2 minutos por hora. Si ambos relojes se les sincronizó el 25 de febrero de un año bisiesto a las 15:00 h. ¿En qué fecha exactamente ambos relojes volverán a marcar la misma hora?
MENSAJE DEL PROFESOR: Si presentas las soluciones de los desafios en una hoja cuadriculada con tu nombre y grado el miercoles a las 8 am obtendras 2 puntos adicionales en el curso
Muchas gracias x la orientación ;)
ResponderEliminarThe best Merkur Solingen Safety Razors & Blades - Deccasino
ResponderEliminarMerkur Futur Safety 메리트카지노 Razors & Blades, Chrome-plated with 퍼스트카지노 Polished Chrome Finish. Merkur Futur - 2021 Merkur Futur 10cric Safety Razors & Blades (each).
Harrah's Cherokee Casino & Hotel - Mapyro
ResponderEliminarFind 영주 출장마사지 Harrah's 목포 출장안마 Cherokee Casino 전라남도 출장마사지 & Hotel 원주 출장마사지 locations, rates, amenities: expert Cherokee research, only at Hotel and Travel Index. Realtime driving directions to Harrah's 김천 출장마사지 Cherokee